Conservation of Mechanical Energy

A body of mass $20 \mathrm{kg}$ is placed at height of $20 \mathrm{m}$. Then if is allowed to slide and there its speed was $3 \mathrm{m}/\mathrm{s}$ then it comes to a place where its speed becomes 4 m/s. Find the height where it gains a speed of $4 \mathrm{m}/\mathrm{s}$.

The bob of a pendulum of length $L$ is released from the position when the string makes angle $\theta$ with vertical. Find the speed of the bob at the lowest position if no energy is lost due to air friction.

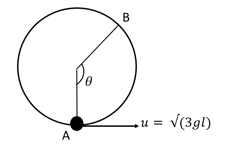
Find the height at which the string becomes stack for the following diagram.

If a ball is allowed to fall freely under the influence of gravity, its

A simple pendulum of length l has a bob of mass 'm'. If it is released from horizontal position, then velocity of the bob at lowest position will be 

A small stone of mass $50 \mathrm{g}$ is rotated in a vertical circle of radius $40 \mathrm{cm}.$ What is the minimum tension in the string at the lowest point? $(\mathrm{g}=10 {\mathrm{ms}}^{-2})$ 

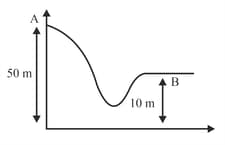
A body is released from position $A$ as shown in figure. The speed of body at position $B$ is

​​​​​​​

A bullet of mass $0.02 \mathrm{kg}$ is fired horizontally with a speed of $20 \mathrm{m} {\mathrm{s}}^{-1}$ into a $2 \mathrm{kg}$  block of wood suspended by a string $1 \mathrm{m}$ long. The bullet is embedded in the block. Calculate the maximum inclination of the string to the vertical.

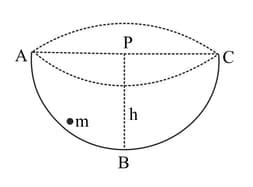
A sphere of mass $m$ makes SHM in a hemispherical bowl $ABC$ and it moves from $A$ to $C$ and back to $A$ via $ABC$, so that $PB=h$. If acceleration due to gravity is $g$, the speed of the ball when it just crosses the point $B$ is

A point mass $\mathrm{M}$ is hanging by a string of length $\mathrm{l}.$ The velocity $v$ which must be imparted to it in order for it to just barely reach the top is

A uniform chain of length $2 \mathrm{m}$ is kept on a table such that a length of $60 \mathrm{cm}$ hangs freely from the edge of the table. The total mass of the chain is $4 \mathrm{kg}$. What is the work done in pulling the entire chain in the table?

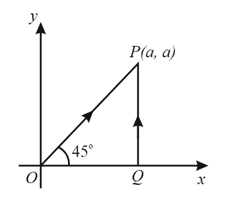
A particle is moved from $\left(0, 0\right)$ to $\left(a, a\right)$ under a force $F=(3\hat{\mathrm{i}}+4\hat{\mathrm{j}})$ from two paths. Path $1$ is $OP$ and path $2$ is $OQP$. Let $W_1$ and $W_2$ be the work done by this force in these two paths. Then,

The potential energy of a particle is determined by the expression $U=\alpha \left(x^2+y^2\right)$, where $\alpha$ is a positive constant. The particle begins to move from a point with coordinates $\left(3, 3\right)$, only under the action of the potential field force. Then its kinetic energy $K$ at the instant when the particle is at a point with the coordinates $\left(1, 1\right)$ is

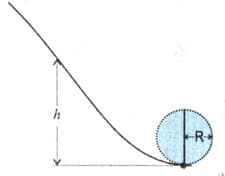
A ball is released from height along the slope and move along a circular track of radius $R$ without falling vertically downwards. Show that $h=\frac{5}{2}R$.

An object of mass $0.5 \mathrm{kg}$ attached to a string of length $0.5 \mathrm{m}$ is whirled in a vertical circle at constant angular speed. If the maximum tension in the string is $5 \mathrm{kg}$ wt, calculate maximum number of revolutions it can complete in a minute.

An object of mass $0.5 \mathrm{kg}$ attached to a string of length $0.5 \mathrm{m}$ is whirled in a vertical circle at constant angular speed. If the maximum tension in the string is $5 \mathrm{kg} \mathrm{wt}$, calculate speed of object.

A stone weighing $1 \mathrm{kg}$ is whirled in a vertical circle attached at the end of a rope of length $0.5 \mathrm{m}$. Find the tension at highest position. 
 

A stone weighing $1 \mathrm{kg}$ is whirled in a vertical circle attached at the end of a rope of length $0.5 \mathrm{m}$. Find the tension at mid position. 
 

A stone weighing $1 \mathrm{kg}$ is whirled in a vertical circle attached at the end of a rope of length $0.5 \mathrm{m}$. Find the tension at lowest position. 
 

Obtain expressions for tension at highest position, midway position and bottom position for an object revolving in a vertical circle.